Increment

Sensitivity Analysis of the increment function establishes its influence on the output of a mathematical model or system (numerical or otherwise). This is a crucial aspect when the sensitivity of a system to uncertain geometry, material properties, manufacturing tolerances, etc. needs to be determined. Based on the results of the sensitivity analysis, inputs important for the design can be focused on.

Theory behind

The sensitivity analysis is performed with Monte Carlo analysis applied directly to the final model and each increment function independently. Each increment function represents an independent contribution to the final statistics, whereas the first-order increment functions ($df_1$, $df_2$ etc.) represent the independent contribution to a given variable, i.e. how the variable alone influences the final problem.

info

Only variance sensitivities of increment functions are computed in the Preliminary Analysis method. Also, sensitivities of increment functions are not available for settings of this method with maximum increment order set to -1**!**

Higher-order increment functions ($df_{1.2}$, $df_{1.3}$, $df_{2.3.4}$ etc.) represent the contribution of interaction effects, i.e. how the interaction between variables influences the final problem. However, higher-order increment function represents only the pure interaction between variables, which means it does not take into account the independent contribution of a given variable.

NOTE

Increment sensitivity only includes the influence of a given sub-domain (increment function of sole variable OR its interaction), while variable sensitivity takes into account all the aspects of a given variable (increment function of the variable AND ALL its interaction effects).

In this program, two sensitivities for an increment function are defined. The first sensitivity is the sensitivity of the mean value, which represents the influence of particular increment function on the final expected value. In other words, how the selected increment function influences the statistical expected value of the final output. The formula for the mean sensitivity estimation is:

$$S_{\mu_{k}}=\frac{\left|\mu_k\right|}{\sum_{j \in S_T}\left|\mu_j\right|}$$

where $S_{\mu_{k}}$ represents the sensitivity of mean for increment function $k$, $S_T$ stands for the set of all increment functions and $\mu_k$ represents the $k$-th increment function. The mean sensitivity feature is not available for the Preliminary Analysis method.

The second type of sensitivity is the variance sensitivity, which represents the variable's impact on the final output. The variable's variance sensitivity is defined as follows:

$$S_{\sigma^2_{k}}=\frac{\left|\sigma^2_k\right|}{\sum_{j \in S_T}\left|\sigma^2_j\right|}$$

where $S_{\sigma_{k}}$ represents the sensitivity of variance for increment function $k$, $S_T$ stands for the set of all increment functions and $\sigma^2_k$ represents the variance of $k$-th increment function. Computed sensitivities are presented in the program as Partial variance and Partial mean.

It should be noted that later the variance sensitivity is normalized, thus, its sum equals $1$. The mean sensitivity is related to the standard deviation of the probability distribution of output values. This measure prevents increment functions from being overrated due to improper scaling.

How to use the interface

There is a collapsible box on the left side of the tab with the opened result file, where the user can set the data to be displayed. Variable and Increment buttons on the top switch between two datasets described in the theory section. In the list of increments below the special focus needs to be paid to interaction effects of input variables - their presence and importance.

It is possible to include or exclude increments from the set of displayed data via checkboxes next to each increment function designation. The selection of items can be also modified with three buttons under the list. The Invert button does the reverse action of all checkboxes in the list. Select all and Unselect all buttons turn all checkboxes on/off.

Two types of output are possible here. Either a tabular view induced with the Text mode button, or the barplot shown switched on by the Visualize mode button.

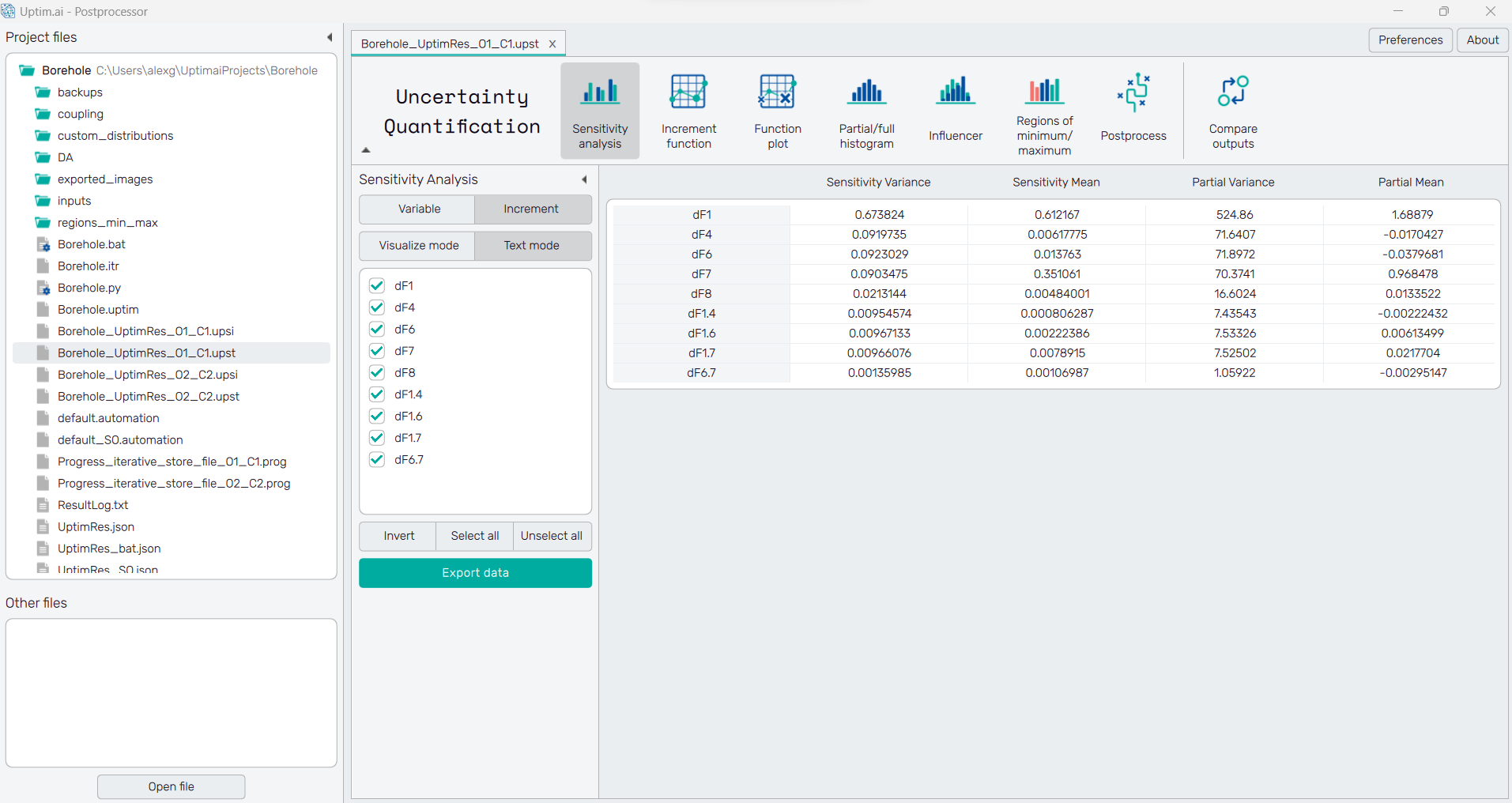
Text mode

The sensitivities of increment functions are presented in the form of a spreadsheet, as shown in Figure 1. It is possible to change the sorting of the sheet(ascending or descending, where ascending is the default) by clicking on the row number or labels of sensitivities.

The green Export data button underneath the list of increment functions saves the currently displayed data into a .csv or .txt file.

Figure 1: Sensitivity Analysis - Increment sensitivity in text mode

Visualize mode

In Visualize mode is the data presented in the form of a barplot, as shown in Figure 2. Users can see a graphical representation of sensitivities for each selected increment function. The sorting of increments in the plot is the same as in the selectable list of increment functions on the left. The presence of mean sensitivities depends on the method used to create the .upst file - it is not available for the Preliminary Analysis method.

Figure 2: Sensitivity Analysis - Increment sensitivity in visualize mode

The green Export data button underneath the list of input variables saves the currently displayed data into a .png or .jpg file. The save-file dialogue can be also induced by the 💾 icon on the top left of the plot. It is possible to adjust the appearance of the plot using controls from the Plot options section of the panel on the left:

• Plot title : Displayed above the plot, Sensitivity Analysis by default.
• X label : Label of the X axis, empty by default.
• Y label : Label of the Y axis, empty by default.
• Title size : Size of the title font.
• Label size : Size of the label font.
• Show legend : Switching on/off the legend of the plot/the colorbar scale.
• Legend font size : Size of the legend font.

Figure 3: Sensitivity Analysis - Plot options of sensitivity analysis